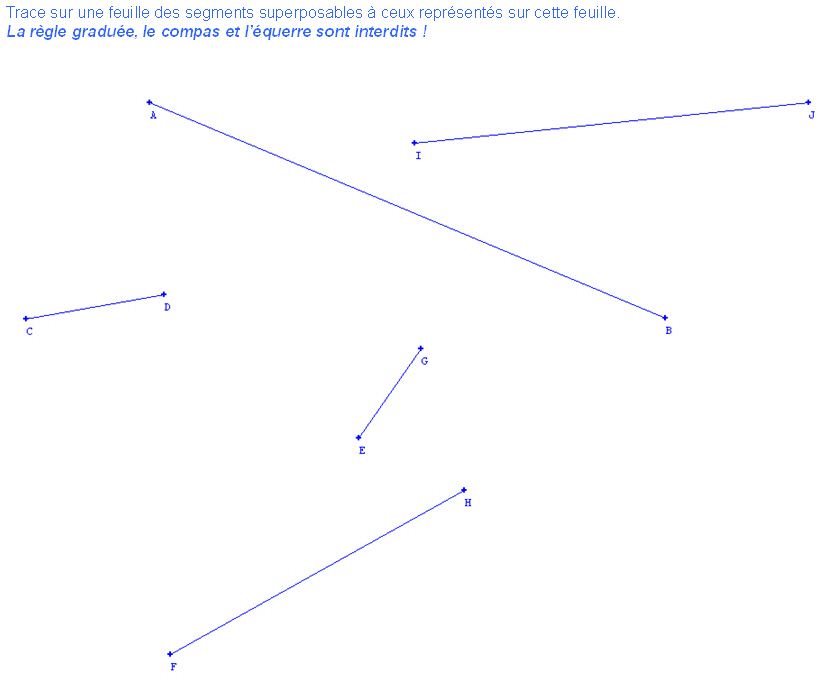
Voici ce que j'ai donné à mes cycles 3 :

Les enfants disposaient d'un crayon de papier, d'une feuille blanche sur laquelle ils devaient reproduire les segments et une feuille (verte) dont j'avais déchiré les contours.
Voici les procédures des enfants par niveau :
Sur mes 3 CE2, deux ont pensé à plier leur feuille et à l'utiliser comme un gabarit de droite... le reste se faisant tout seul.
La troisième utilisait la feuille verte sans la plier, en y reportant dessus - à un endroit où la feuille verte avait été déchirée un peu près droit - les extrémités du segment à reproduire :

Ensuite, elle reportait ces deux extrémités sur sa feuille blanche et les reliait à main levée.
Sur 5 CM1, 2 d'entre-eux ont tout de suite et sans aucune hésitation plié leur feuille et fini le travail rapidement.
2 autres ont fini par faire le geste de pliage après un petit temps de réflexion. Bref pour ces quatre là, cette situation n'avait rien de
problématique.
Le cinquième est parti dans une procédure tout à fait personnelle mais payante, en voici les étapes :
1) Pour commencer, il a tenté d'utiliser la feuille verte comme un calque en essayant donc de décalquer le segment à reproduire... Pas de chance, impossible de voir quoi que ce soit de net. L'idée commence à montrer ses limites.
2) Persuadé qu'il est sur la bonne piste, il commence à faire un trou dans la feuille verte (avec la pointe de son crayon) :

Son idée était de créer une fente dans sa feuille verte de la longueur du segment à reproduire. Ensuite, il tracé sur sa feuille blanche un trait en plaçant son crayon dans le trou qui avait fait dans sa feuille verte (c'est l'idée du pochoir...).
3) Pas du tout satisfait du résultat, il s'est lancé dans une autre procédure. A l'instar de l'élève de CE2, il n'a pas plié sa feuille verte et a reporté sur les bords de sa feuille verte les extrémités des segments. Il les a reportés sur sa feuille blanche. Il ne lui restait plus qu'à les relier.
4) Après quelques essais, il a plié... sa feuille blanche sur laquelle les segments devaient être reproduits. Ainsi, il a utilisé les bords de sa feuille blanche A4 comme d'une règle.

Il lui suffisait de faire en sorte, lors de son pliage, que le bord de sa feuille blanche passe par les deux extrémités du
segment qu'il venait de reporter.
A la fin, sa feuille blanche était pliée dans tous les sens mais les segments étaient justes !
Je lui ai demandé d'aller reproduire le segment [AB] au tableau :
"Impossible, je ne peux pas plier le tableau !" m'a-t-il répondu.
Pour mes 5 CM2, cette séance était une promenade de santé ! A peine les feuilles distribuées que les pliages avaient commencé !
Ce qui est drôle, c'est que leurs pliages ont abouti à l'élaboration d'un "gabarit de règle". Au départ, ils n'ont plié qu'une
seule fois puis progressivement, leur feuille verte a pris la forme de règle.

J'ai laissé chacun à sa méthode...
Ensuite , j'ai demandé aux enfants de vérifier que leurs segments correspondaient bien aux segments que je leur avais donnés.
Le papier calque est sorti des pochettes (depuis le temps qu'ils demandaient quand on allait l'utiliser...) !
Certains ont reproduit les segments sur le calque avec leur méthode et ont comparé les segments de leur feuille blanche
avec ceux du calque et de la feuille d'énoncé.
D'autres ont reporté sur leur claque uniquement les extrémités des segments de la feuille d'énoncé et les ont comparés avec
leurs segments produits.
Un seul élève (un CE2) a utilisé la transparence de sa feuille blanche pour superposer ses segments à ceux de l'énoncé.
Pour finir, chacun a exposé sa méthode. Le pliage de la feuille verte s'est montré la procédure la plus efficace aux yeux des enfants.
Armand (8/02/07) : Est-ce que dans cette phase de vérification, le compas était également explicitement interdit ? En effet cela pose la question générale de la perception par les élèves ( comme par nous-mêmes ... ) des limites ou du cadre de contrat pédagogique plus ou moins implicite sur les ressources et outils qu'on apotentiellement le "droit" d'utiliser dans une situation problème donnée. Il y a-t-il eu, en dehors de la consigne écrite qui interdisait l'usage dela règle , de l'équerre et du compas, et du matériel lui-même distribué ( feuille verte et crayon ), une reformulation orale qui interdisait aussi le recours au papier calque ? Autrement dit pour tous ces problèmes où nous testons le réinvestissement possible d'acquis antérieurs, notamment dans le cadre scolaire, quelle est la part qui révèle une accessibilité de l'élève à ses propres acquis antérieurs et quelle est la part qui révèle simplement sa perception de la "commande" scolaire du maître, même dans le cas où le maître, comme ici, est très attentif à la construction de l'autonomie intellectuelle des élèves.
Céline (10/02/07) : La règle, le compas et l'équerre ont été interdits pour la première phase mais comme j'avais demandé aux enfants de ranger tout cet attirail, les enfants ne l'ont pas ressorti. A aucun moment le calque n'a été interdit. Mais dans la première phase, les enfants ont travaillé uniquement avec la feuille verte puisque, comme tu le dis, nous étions dans un "contrat pédagogique". Pour la phase de vérification, j'ai sûrement induit beaucoup de choses en pointant le mot "superposables". Et puis, il suffit qu'un élève sorte une feuille de papier calque pour que tous les élèves en sortent une. Mais la "commande" scolaire du maître que tu pointes à juste titre est toujours plus ou moins présente, ce qui gêne parfois, même si mon travail consiste à ouvrir un champ de libertés suffisamment grand pour que chacun puisse s'investir dans les tâches proposées avec ses procédures personnelles.
Cette séance fait suite à un travail sur les "gestes instruments".
Pour commencer, nous avons fait un petit rappel de ce que nous avions vu lors du travail sur les "gestes instruments".
Ensuite, je leur ai dit que nous allions nous engager dans un travail en géométrie, et que pour cela, nous avions besoin de
nous mettre d'accord sur quelques règles :
Ma feuille déchirée représente un plan et je leur explique que les parties déchirées peuvent "s'étirer à l'infini" :
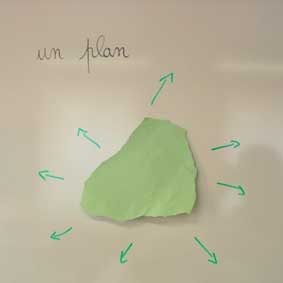
Merci à Leplus pour le cours :
"On pourrait aussi déverser lentement de l'eau sur une table et inviter le groupe à rêver d'un liquide magique s'étendant à l'infini."
J'ai donc repris cette image avec les enfants, car je la trouve extrêmement parlante et les élèves sont vite entrés dans ce que
je leur proposais.
En pliant notre feuille (comme dans notre séance précédente, la notion de demi-plan apparait facilement. En effet, puisque
celle la partie déchirée s'étire, la notion de frontière est vite apparue évidente aux enfants.
Avec mes élèves, j'ai utilisé l'idée que du côté déchiré, je peux me promener librement et aller où je veux, comme un français qui
a le droit de se promener n'importe où en France. Par contre, si je souhaite traverser la limite fixée par le côté plié, je dois
avoir un passeport (bon, d'accord, l'ouverture des frontières ne suit pas cette logique mathématique, mais bon...).
Je leur ai demandé comment s'appelle cette "limite" : un CM1 m'a rapidement donné le mot "fontière".
L'histoire de notre demi-plan s'arrête là. Je fixe la feuille pliée au tableau et écris le vocabulaire : demi-plan et frontière.
Ensuite, je plie une deuxième fois ma feuille pour faire apparaître
un secteur angulaire. D'ailleurs, il est vite apparu aux enfants que c'était de ça qu'il s'agissait car
mes CM2 a été quelques uns a utilisé le mot "angle" devant mon pliage.
Puisque notre règle est de dire que du
côté déchiré, ça s'étend à l'infini, je décide de mettre mon secteur sur un table et je dis aux enfants que tous
ceux qui sont dans le secteur angulaire sont morts. Alors là, j'ai eu du succès ! Certains sont sûrs de leur sort,
s'effondrent sur leurs tables en rigolant. Et moi, je me dis que je commence à gagner sur cette idée qu'en
géométrie, les objets peuvent s'étendrent à l'infini... Le sort de quelques uns est indéfini, comment savoir ?
Un enfant propose de prolonger les frontières à l'aide d'un ficelle : aussitôt dit, aussitôt fait, je vais chercher un pelote de laine dans l'armoire et lui lance : "et bien, vas-y !".
Il étire sa laine et le sort des enfants tombe : un seul échappe au secteur !
Certains imaginent à voix haute un jeu dans la cour où chacun aurait un secteur angulaire à dégainer pour éliminer ceux qui sont pris dedans ! Comme un rayon laser ! Même qu'ils l'appeleraient le jeu du "secteur-loup" !
J'ai invité les enfants à faire leurs propres pliages. Chacun s'empare d'une feuille et nous fixons le tout au tableau :

Certains ont déjà créé des angles droits,
mais j'ignore délibérément la chose pour le moment.
Je leur demande combien on peut trouver de secteurs angulaires
différents.
Alors là, certains proposent une infinité, d'autres un nombre fini (10, 1000...).
Les discussions
vont bon train mais ils finissent par se mettre d'accord sur le fait qu'on peut toujours en créer un différent de
ceux que nous avons fixé au tableau.
La suite s'imagine facilement grâce à ces photos.
Nous nous rendons dans la
cour pour déterminer l'intersection de deux secteurs angulaires.
Je fixe deux secteurs avec du scotch dans la cour
et je demande aux enfants de déterminer l'endroit où se "croisent" les deux secteurs. Ils ont de la ficelle et
des craies.




Un quadrilatère apparaît :

Nous nous arrêtons là... ça fait déjà beaucoup pour une séance !
Petit exercice :

Consigne : Classe les secteurs angulaires
Alors là je suis ouverte à toutes les critiques...
Suite à la séance 1, je me demande ce que les enfants ont retenu de nos pliages et de notre escapade dans la cour avec nos
gabarits d'angles, nos ficelles et nos craies.
Je décide donc de leur donner ce petit exercice.
Le mot "classe" décontenance les élèves... Ils ne voient pas bien où je veux en venir.
Je prends l'exemple de leur classe : ils sont ensemble parce qu'ils ont quelque-chose en commun. Ils sont inscrits à l'école de
Bannes. Aucun autre enfant, inscrit dans une autre école, ne peut venir dans leur classe.
Je n'ai pas choisi ce mot "classe"
par hasard : dans ma tête, il est clair que je veux les amener à construire des classes d'équivalence.
Je leur demande donc de trouver "un point commun" entre ces secteurs angulaires qui permettrait de les mettre dans une
même classe.
"Ben s'ils sont superposables, ils vont ensemble !" lance Arnaud.
Deux techniques sont alors
mises en place : le découpage et le décalquage. Les deux sont payantes.
De toute façon, je ne m'attendais pas à ce
que ça pose de problème particulier.
Les enfants ne se mettent pas d'accord sur le nombre de classes
différentes. Ils hésitent entre 3, 4 et 5.
Puis un bilan collectif permet de conclure.
Commentaire : J'aime assez cette idée de présenter les secteurs angulaires de cette façon.
Et comme je suis plutôt du genre à appeler un chat un chat, nous avons établi 4 ensembles que j'ai nommé respectivement classe 1,
classe 2, classe 3 et classe 4.
Lorsque j'ai demandé "Alors combien y-a-t-il de secteurs angulaires différents ?", les élèves ont répondu
sans hésitation 4. Ce qui sous-entend qu'ils perçoivent l'idée de "représentant" d'une classe
d'équivalence.
Mais suis-je sur la bonne voie ? J'abuse peut-être avec cette idée de classe.
Et puis à la
question "combien existe t-il de classes différentes ?", les enfants répondent tout aussi facilement que
précédemment "une infinité !".
Mais je ne suis pas entièrement satisfaite de cette séance. Je me suis égarée
par rapport à mon projet initial...
Mais bon.
Quelques commentaires de Leplus seraient les bienvenus !
Leplus : (04/04/07) Je proposerais plutôt ceci :

et je préciserais que sur la
feuille sont représentés des fragments de secteurs. Il faut toujours dans un premier temps être attentif au fait que
les enfants identifient l'objet géométrique à ce qu'il voient. Donc en l'occurrence réduisent leur conception du
secteur aux seules "demi droites". Le secteur se réalise comme intersection de deux demi plans. C'est donc un
morceau de plan et rien n'est mieux qu'un morceau de feuille coloré pour représenter le secteur. Les livres qui ne
représentent que les "côtés" semblent travailler sur un à priori implicite d'écartement. La démarche que
propose Céline et comparable à celle qui, à partir de tris de "traits droits" construit le concept de longueur
comme classe d'équivalence de segments isométriques. Avec les secteurs, elle approche l'angle comme classe
d'équivalence de secteurs "superposables". Ce sont là deux situations illustrant parfaitement la démarche
proposée dans les IO. Toutes d'eux mettent en évidence la nécessité d'une utilisation raisonnée de gestes-instrument
(découper-superposer) ou d'instrument (le calque)
Si le mot classe fait obstacle on peut contourner en
proposant de trier les secteurs et revenir après sur un lexique possible (famille, classe, angle). Il est très
pertinent de travailler avec des référents de "surfaces différentes". C'est en effet par la perception d'un même
malgré de l'autre qu'il sera possible de proposer le terme d'écartement ou d'angle. En opérant ainsi Céline
travaille en profondeur le concept de grandeur. Leplus ne peut que s'en réjouir et ses employeurs aussi."
Céline : Bon effectivement, j'ai intérêt à rester dans la lignée des manipulations.
Ce qui devrait me rassurer, c'est que lors du bilan, j'ai découpé mes secteurs angulaires de la sorte pour les ranger ensemble :
ça limite les dégâts !
Pour cette séance, je décide de recentrer d'avantage nos activités géométriques sur la manipulation.
Je distribue à chaque élève une feuille rose et une feuille verte et je leur demande de créer, à leur guise, deux
gabarits de secteurs angulaires.
Ils s'exécutent sans problème.
Ensuite, je leur demande de "jouer" avec ces 2 gabarits en les "croisant" de différentes manières (pas satisfaite de cette consigne...) et d'essayer de faire des observations, de rechercher tout ce qui peut arriver.
Personnellement, je pensais qu'ils reproduiraient sur une feuille ce qu'ils avaient
vécu dans la cour, avec des secteurs angulaires qui forment un quadrilatère.
Et bien la suite m'a prouvé qu'il faut que j'arrête de penser... et qu'il faut que je laisse du temps aux choses pour s'installer.
Les enfants étaient bien embarassés avec ce que je leur demandais. Moi-même, je pense que je pédale dans la semoule !
Ils ne se sont pas appropriés la liberté qui leur était offerte de se lancer dans de telles recherches...
Et puis une CE2 m'appelle et me dit qu'elle remarque quelque-chose de particulier lorsqu'elle rapproche ses deux gabarits :
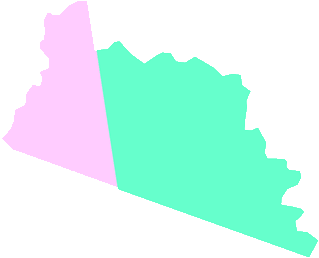
Je bénis le hasard des pliages et je lui demande ce qu'elle observe de particulier : "c'est tout droit ici." me dit-elle en pointant les parties non déchirées.
J'approuve son observation et je l'invite à regarder l'affichage de la classe sur lequel on voit
différents collages légendés : plan, demi-plan et secteur angulaire. Ces affichages ont été réalisés en début de la
séance précédente en guise de rappel.
Elle y retrouve le mot qu'elle cherchait : "ça forme un demi-plan."
Comme je sens la classe dans un désarroi total, je demande à cette élève d'aller placer sa trouvaille au
tableau afin que tout le monde puisse l'observer.
Les enfants perçoivent tout de suite ce qui se passe. Les deux secteurs forment bien un demi-plan.
Mon côté "je ramène ma science" précise qu'en géométrie, les deux angles sont dits supplémentaires. (Maintenant, je me demande si tout ce vocabulaire est nécessaire...)
Leplus: Il n'est pas prioritaire. Cependant, dans des situations "extraordinaires" de ce type il peut être intéressant pour des enfants de l'entendre prononcer par l'adulte et d'associer l'évènement à un mot juste plutôt qu'à la couleur de la mini-jupe de la maîtresse.
Mon côté tout aussi bavard demande aux enfants que certes que l'on peut parler d'un demi-plan mais que si je considère qu'il s'agit d'un secteur angulaire, on lui donne un nom particulier : le secteur angulaire plat
Leplus: Il faut arrêter de se culpabiliser sans cesse. Un adulte, avec sa parole d'adulte, peut parler ainsi aux enfants. C'est à mon sens une façon de signaler l'existence d'autres territoires à conquérir. Il est temps d'arrêter de croire que les enfants ne doivent entendre que les mots qu'ils connaissent pour s'intéresser au monde .. Quipudep et ses amis de Bannes (Tes élèves d'ailleurs) ne me contrediraient pas .
Toujours en étant trop bavarde, je demande aux enfants ce qui arrive si les deux angles sont égaux.
Les enfants ont perçu qu'on aboutissait à des secteurs angulaires droits.
Nous nous sommes arrêtés sur la réalisation d'un affichage pour la classe (promis, je ramène une photo).
Les termes 180° et 90° ont été prononcés par les enfants, nous l'avons écrit sur ces affichages.
Commentaires : Je ne sais pas bien où je vais.
1) Comment être moins directive et comment rendre les enfants chercheurs face à ces objets.
2) Quel niveau de formulation ? Quel vocabulaire ?
Cher Leplus, là j'ai besoin d'aide ! Je ne sais pas si je propose quelque-chose qui tient la route à mes élèves !
S.O.S. !
Les plumes ( après sa sieste) : Ce n'est pas toujours
facile quand on rentre dans ce type de situations très ouvertes de réagir dans l'instant. Ce n'est pas grave
d'ailleurs car on peut toujours revenir sur tout ce qui s'est passé. La vie est longue. Le hasard heureux ( qu'on
pourrait par ailleurs provoquer) est l'occasion d'une relance pour une séance à venir. Dans l'instant, tu aurais
pu interroger les autres sur leur possibilité d'en faire autant. Ce qui ouvrait sur une petite situation problème
intéressante sollicitant un usage raisonné de mes instruments favoris; Le gabarit de droite (un vieux bout de
feuille pourrie mais "pliée-tendue" dans la bonne tradition du geste instrument) et le calque.
Situations possibles (en image ici mais en Canson sous la pluie):

On peut par exemple déclarer que tous ont voulu faire un demi plan comme cette élève de CE2, mais ont cru qu'il suffisait de coller côte à côte des secteurs. De plus ils ont scotché leurs travaux. Que pourraient-ils essayer de faire pour obtenir des "secteurs plats" sans retirer le scotch et sans utiliser de papier supplémentaire.
Ou encore dans le même registre de situations justifiant d'un usage raisonné des instruments: on donne ceci :

et on demande cela :

Plus précisément le gabarit
jaune et le gabarit violet qui donnent cela ! Et cela dissimule bien entendu un secteur droit. (jaune et rouge ou
vert et violet mais pas nécessairement jaune et violet. Faudrait voir à ne pas exagérer quand même. Quoique...
Quand à la formulation elle se construira corrélativement à "l'intelligence" des gestes.
Bon courage.
Céline : Merci pour ce coup de pouce ! Pas facile, facile tout ça. Il faut que je laisse sur le quai
ma valise d'ancienne élève ayant vécu subit la géométrie comme un calvaire pour enfin m'amuser avec les
feuilles "pourries" leplussiennes ! Alors :
1) Ok, je ne laisse pas tomber mon côté "je ramène ma science"
parce-que ça fait partie de ma personnalité et que premièrement aucun élève n'est traumatisé à vie et que
deuxièmement, je sais bien que ce qui importe, ce n'est pas que les enfants aient retenu le mot "supplémentaire"
mais qu'ils approchent le fait qu'un demi-plan peut être construit à l'aide de deux secteurs angulaires, ou plus
si affinités.
2) J'ai réalisé que pour obtenir des secteurs angulaires obtus avec nos pliages, l'assemblage de
nos gabarits est nécessaire.
3) J'ai de la matière pour poursuivre : je vais distribuer un gabarit différent de
secteur angulaire à chaque élève et à lui de construire le secteur angulaire supplémentaire (en interdisant règle,
équerre, compas), puis complémentaire... Je sais que je vole sans honte et sans complexe les propositions de ce cher
Leplus. Mais bon, je dis merci parce que bon, faut pas pousser ! Alors MERCI !
4) Et pourquoi pas ne pas exagérer justement ?
A bientôt pour la suite (des deux mains !)
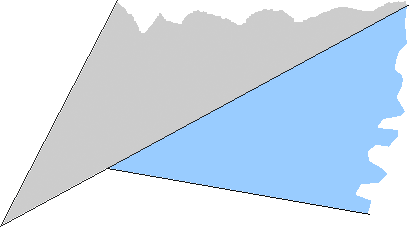
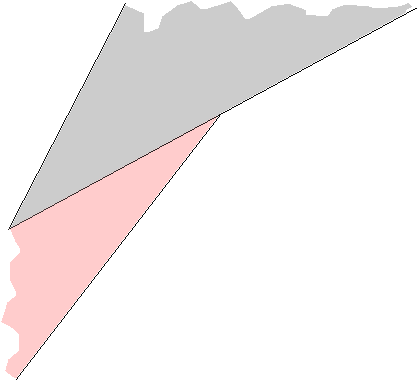
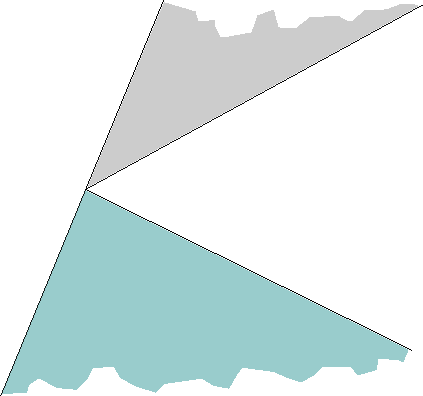
J'ai distribué à chaque élève un secteur angulaire (chaque élève avait un secteur différent) comme ceux-ci :
Puis je leur ai demandé de construire
le gabarit du secteur angulaire qui est supplémentaire à celui qu'ils ont, autrement dit le gabarit du secteur
angulaire qui leur permet d'obtenir un demi-plan lorsqu'on les place côte à côte.
Voici ce que j'ai obtenu :








A méditer pour la suite...
En attendant, je prends tout commentaire !
Au fait, voici l'affichage qui est dans ma classe et qui sert aux enfants (enfin, j'espère) :
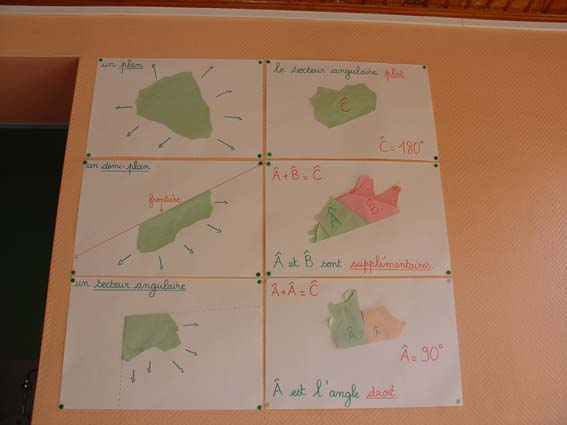
Pour le moment, c'est la seule trace écrite qui nous reste de ces séances de géométrie.
Sur les conseils de Leplus, voici ce que j'ai proposé aux enfants pour cette séance :
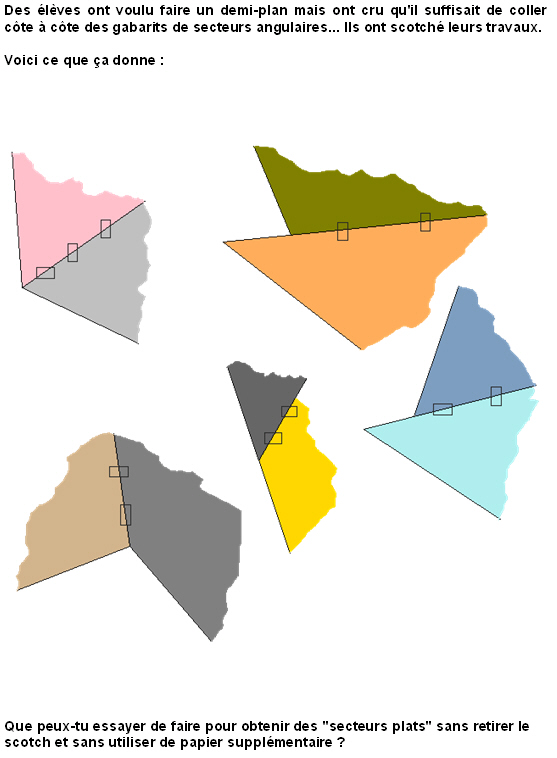
Voici ce que ça donne :
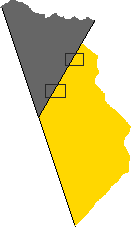
Pour ce gabarit, aucun problème, les enfants remarquent qu'il s'agit bien d'un secteur angulaire plat et certains le vérifient spontanément avec leurs règles.
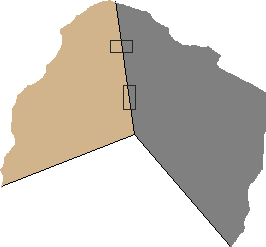
Aucun problème pour celui-ci aussi, les deux réponses données sont les suivantes :

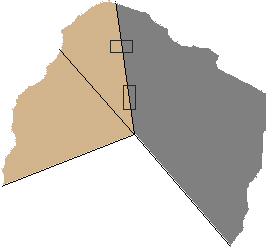
Les élèves prolongent l'une des demi-droites.
C'est pour les autres gabarits que tout se complique !
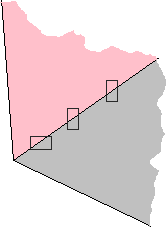
Ici, les enfants proposent ceci :
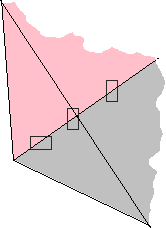
ou cela (en décalquant, en découpant et en pliant) :
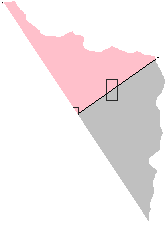
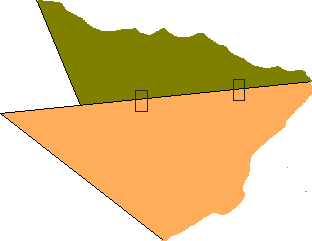
Ici, les élèves proposent ces solutions :
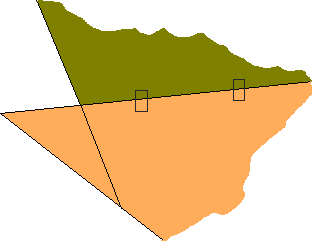
Et pour finir :
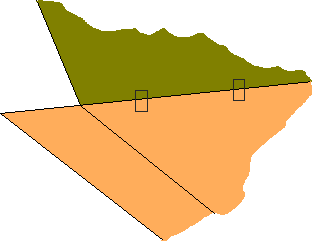
Mêmes erreurs :
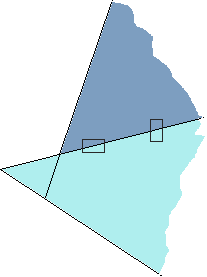
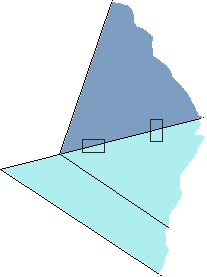
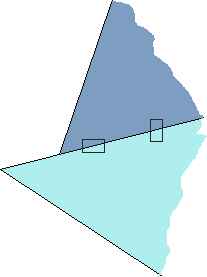
Un CM2 s'est cependant orienté vers une piste originale :
Il a découpé le secteur angulaire bleu clair :
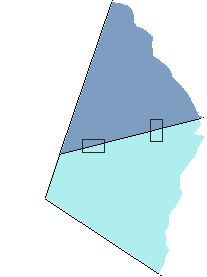
Et il l'a associé à un autre gabarit :
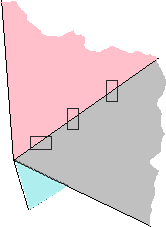
Bref, rien n'est gagné, loin de là !
Remarques avant d'aller me pendre un peu avant la prochaine séance :
1) L'idée de "prolongement à
l'infini" est loin d'être acquise car lorsque les enfants découpaient, ils prenaient soin de bien suivre les
gabarits, même du côté déchiré...
Cependant, ils touchent l'idée que les "enjeux" sont au niveau des demi-droites des secteurs angulaires car
leurs propositions portaient sur celles-ci.
2) Par contre, prendre en compte
que ces demi-droites ou frontières se prolongent également est plus difficile.
3) J'ai décidé de ne pas poursuivre
plus loin avec mes CE2 en géométrie sur ce travail... il semblerait que ce soit trop tôt.
Céline Guillemin